SciPy - Poisson Distribution

Poisson Distribution is a discrete probability distribution and it expresses the probability of a given number of events occurring in a fixed interval of time or space if these events occur with a known constant mean rate and independently of the time since the last event.

The probability mass function (pmf) of poisson distribution is defined as:

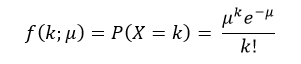
Where, k is the number of occurrences (k=0,1,2...), μ is average number of events.

An poisson distribution has mean μ and variance μ.

The cumulative distribution function (cdf) evaluated at k, is the probability that the random variable (X) will take a value less than or equal to k. The cdf of poisson distribution is defined as:

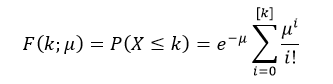
Where, [k] is the greatest integer less than or equal to k.

The scipy.stats.poisson contains all the methods required to generate and work with a poisson distribution. The most frequently methods are mentioned below:

Syntax

scipy.stats.poisson.pmf(k, mu, loc=1)
scipy.stats.poisson.cdf(k, mu, loc=1)
scipy.stats.poisson.ppf(q, mu, loc=1)
scipy.stats.poisson.rvs(mu, loc=0, size=1)

Parameters

poisson.pmf()

The poisson.pmf() function measures probability mass function (pmf) of the distribution.

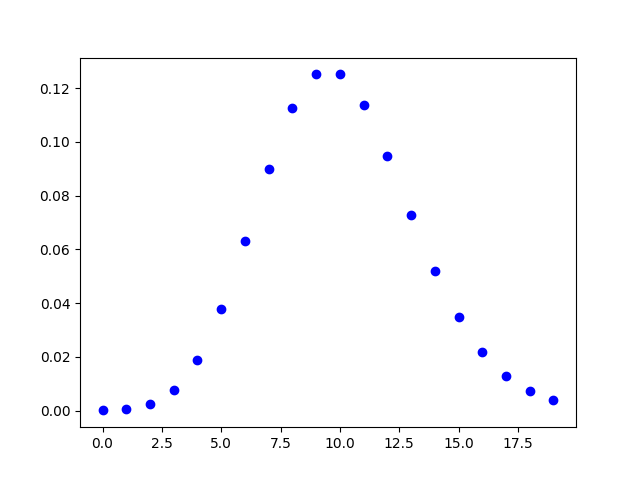
from scipy.stats import poisson
import matplotlib.pyplot as plt
import numpy as np

#creating an array of values between
#0 to 20 with a difference of 1
x = np.arange(0, 20, 1)
   
y = poisson.pmf(x, 10, 0)
   
plt.plot(x, y, 'bo') 
plt.show()

The output of the above code will be:

poisson.cdf()

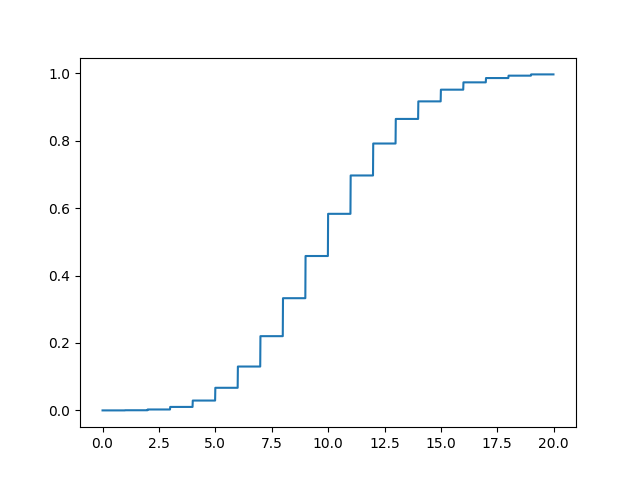
The poisson.cdf() function returns cumulative distribution function (cdf) of the distribution.

from scipy.stats import poisson
import matplotlib.pyplot as plt
import numpy as np

#creating an array of values between
#0 to 20 with a difference of 0.01
x = np.arange(0, 20, 0.01)
   
y = poisson.cdf(x, 10, 0)
   
plt.plot(x, y) 
plt.show()

The output of the above code will be:

poisson.ppf()

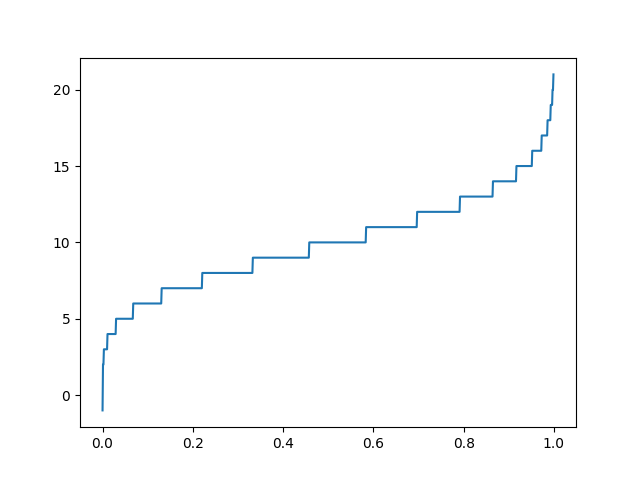
The poisson.ppf() function takes the probability value and returns cumulative value corresponding to probability value of the distribution.

from scipy.stats import poisson
import matplotlib.pyplot as plt
import numpy as np

#creating an array of probability from
#0 to 1 with a difference of 0.001
x = np.arange(0, 1, 0.001)
   
y = poisson.ppf(x, 10, 0)
   
plt.plot(x, y) 
plt.show()

The output of the above code will be:

poisson.rvs()

The poisson.ppf() function generates an array containing specified number of random values drawn from the given poisson distribution. In the example below, a histogram is plotted to visualize the result.

from scipy.stats import poisson
import matplotlib.pyplot as plt
import numpy as np

#fixing the seed for reproducibility
#of the result
np.random.seed(10)

#creating a vector containing 10000
#random values from poisson distribution
y = poisson.rvs(10, 0, 10000)

#creating bin
bin = np.arange(0,25,1)  

plt.hist(y, bins=bin, edgecolor='blue') 
plt.show()

The output of the above code will be: