SciPy - Integrate

The scipy.integrate sub-package provides several integration techniques including an ordinary differential equation integrator. The most commonly used methods and interfaces of this package are listed below:

Methods for Integrating Functions given function object
quad	General purpose single integration
dblquad	General purpose double integration
tplquad	General purpose triple integration
nquad	General purpose n-fold multiple integration
fixed_quad	Integrate func(x) using Gaussian quadrature of order n
quadrature	Integrate with given tolerance using Gaussian quadrature
romberg	Integrate func using Romberg integration
Methods for Integrating Functions given fixed samples
trapezoid	Use trapezoidal rule to compute integral
cumulative_trapezoid()	Use trapezoidal rule to cumulatively compute integral
simpson	Use Simpson's rule to compute integral from samples
romb	Use Romberg Integration to compute integral from (2^k + 1) evenly-spaced samples
Interface to numerical integrators of ODE systems
odeint	General integration of ordinary differential equations
ode	Integrate ODE using VODE and ZVODE routines

Single Integration

The scipy.integrate.quad() function is normally the default choice for performing single integral of a function. It integrates a function func over a given range from a to b. The syntax for using this function is given below:

Syntax

scipy.integrate.quad(func, a, b, args)

Parameters

`func`	`Required.` Specify a Python function or method to integrate.
`a`	`Required.` Specify lower limit of integration.
`b`	`Required.` Specify upper limit of integration.
`args`	`Optional.` Specify extra arguments to pass to func.

Example: Single integration

In the example below, the quad() function is used to compute the following single integral:

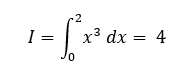
from scipy.integrate import quad

#creating a function that need 
#to be integrated (integrand)
f = lambda x: x**3

#integrating the function
I = quad(f, 0, 2)

#displaying the result
print(I)

The above example returns two values. The first value is the result of integration and the second value is an estimate of the absolute error in the result. The output will be:

(4.0, 4.440892098500626e-14)

Example: Passing arguments to integrand

Consider one more example, where arguments are passed to the integrand.

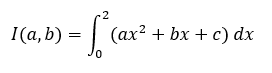
from scipy.integrate import quad

#creating the integrand
def func(x, a, b, c):
  return a*x**2 + b*x + c

#integrating the function x*x + 2x + 3 
I1 = quad(func, 0, 2, args=(1, 2, 3))

#integrating the function 2*x*x + 5x + 7 
I2 = quad(func, 0, 2, args=(2, 5, 7))

#displaying the result (first element
# of returned tuple)
print(I1[0])
print(I2[0])

The output of the above code will be:

12.666666666666666
29.333333333333336

Multiple Integration

The mechanics for double and triple integration is wrapped into the functions dblquad and tplquad. These functions take the function to integrate and four, or six arguments, respectively. The limits of all inner integrals need to be defined as functions.

Double Integration

The scipy.integrate.dblquad() function computes a double integral. It returns the double (definite) integral of func(y, x) from x = a..b and y = gfun(x)..hfun(x). The syntax for using this function is given below:

Syntax

scipy.integrate.dblquad(func, a, b, gfun, hfun, args)

Parameters

`func`	`Required.` Specify a Python function or method to integrate. It must have at least two variables: y must be the first argument and x the second argument.
`a`	`Required.` Specify lower limit of integration of x.
`b`	`Required.` Specify upper limit of integration of x.
`gfun`	`Required.` Specify the lower boundary curve in y which is a function taking a x as argument.
`hfun`	`Required.` Specify the upper boundary curve in y which is a function taking a x as argument.
`args`	`Optional.` Specify extra arguments to pass to func.

Example: Double integration

In the example below, the dblquad() function is used to compute following double integral:

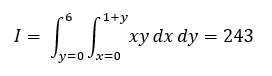
from scipy.integrate import dblquad

#creating a function that need 
#to be integrated (integrand)
f = lambda x, y: x*y

#creating lower and upper boundary 
#curve in y as a function of x
lfunc = lambda x: 0
ufunc = lambda x: 1+x

#integrating the function
I = dblquad(f, 0, 6, lfunc, ufunc)

#displaying the result
print(I)

The above example returns two values. The first value is the result of integration and the second value is an estimate of the absolute error in the result. The output will be:

(243.0, 2.6978419498391304e-12)

Example: Passing arguments to integrand

Consider one more example, where arguments are passed to the integrand.

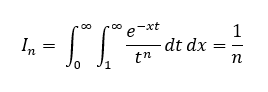
from scipy.integrate import dblquad
import numpy as np

#creating the integrand
def func(t, x, n):
  return np.exp(-x*t) / t**n

#integrating the function for n=2
I1 = dblquad(func, 0, np.inf, 1, np.inf, args=(2,))

#integrating the function for n=5
I2 = dblquad(func, 0, np.inf, 1, np.inf, args=(5,))

#displaying the result (first element
# of returned tuple)
print(I1[0])
print(I2[0])

The output of the above code will be:

0.4999999999985751
0.2000000000189363

In addition to the functions described above, scipy.integrate sub-package has a number of other integration functions, including nquad, which performs n-fold multiple integration, as well as other functions that implement various integration algorithms. However, quad and dblquad is most frequently used functions.