Algorithms

Algorithms

Heap Sort

Heap sort uses property of heap to sort the array. It involves building a max heap for increasing order sorting which contains largest element of the heap at the root. For decreasing order sorting min heap is used which contains smallest element of the heap at the root. The process step of for increasing order sorting of heap sort is summarized below:

Step 1: Build a max heap which contains largest element of the heap at the root
Step 2: Swap the last element of heap with root element and remove the last element from the heap. With the remaining elements repeat the step 1.

Example:

To understand the heap sort, lets consider an unsorted array [10, 1, 23, 50, 7, -4] and discuss each step taken to sort the array in ascending order.

In the below figure, the heap structure of input array and max heap is shown. The index number of the root element of the heap is 0. In max heap, the largest element of the heap always resides at the root.

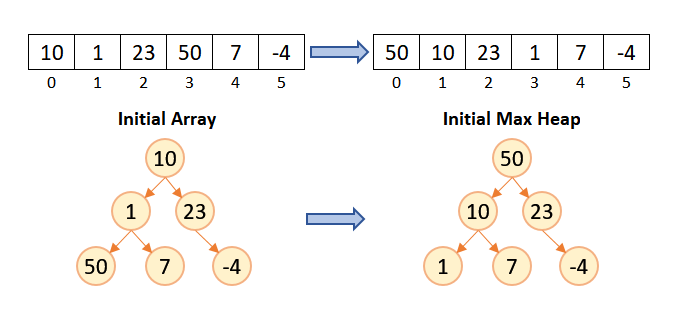
heap Sort Diagram

After building the initial max heap, the last element of heap is swapped with the root element and the last element which contains the largest number of the array is removed from the heap. After that, the heapify function is used on the remaining elements of the heap to make it as a max heap and the number of elements will reduce by one. This process is continued until the number of elements in the heap is one. At this point, the array will be sorted.

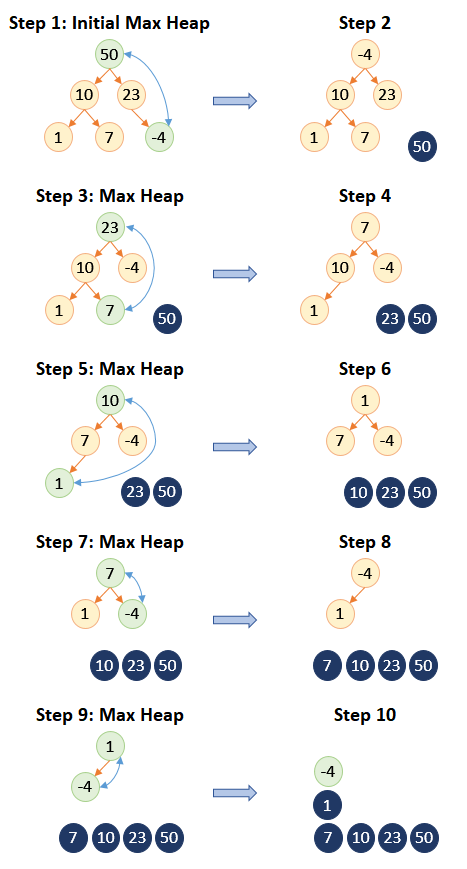
heap Sort

The above figure describes elimination of largest element from the heap and formation of the max heap from the remaining elements of the heap. The final outcome of the process is an increasing order sorted array.

Implementation of Heap Sort

# function for heap sort which calls heapify function 
# to build the max heap and then swap last element of 
# the max-heap with the first element
# exclude the last element from the heap and rebuild the heap
def heapsort(MyList):
  n = len(MyList)
  for i in range(n//2, -1, -1):
    heapify(MyList, n-1, i)

  for i in range(n-1, -1, -1):
    # swap last element of the max-heap with the first element
    MyList[i], MyList[0] = MyList[0], MyList[i]
    
    # exclude the last element from the heap and rebuild the heap 
    heapify(MyList, i-1, 0)

# heapify function is used to build the max heap
# max heap has maximum element at the root which means
# first element of the array will be maximum in max heap
def heapify(MyList, n, i):
  max, left, right = i, 2*i + 1, 2*i + 2
  # if the left element is greater than root
  if left <= n and MyList[left] > MyList[max]:
    max = left

  # if the right element is greater than root
  if right <= n and MyList[right] > MyList[max]:
    max = right

  # if the max is not i
  if max != i:
    MyList[i], MyList[max] = MyList[max], MyList[i]
    # Recursively heapify the affected sub-tree
    heapify(MyList, n, max) 

# function to print list
def PrintList(MyList):
  for i in MyList:
    print(i, end=" ")
  print("\n")
  
# test the code                 
MyList = [10, 1, 23, 50, 7, -4]
n = len(MyList)
print("Original List")
PrintList(MyList)

heapsort(MyList)
print("Sorted List")
PrintList(MyList)

The above code will give the following output:

Original List
10 1 23 50 7 -4 

Sorted List
-4 1 7 10 23 50

public class MyClass {
  // function for heap sort which calls heapify function 
  // to build the max heap and then swap last element of 
  // the max-heap with the first element
  // exclude the last element from the heap and rebuild the heap
  static void heapsort(int Array[]) {
    int n = Array.length;
    int temp;

    for(int i = n/2; i >= 0; i--) {
      heapify(Array, n-1, i);
    }

    for(int i = n - 1; i >= 0; i--) {
      //swap last element of the max-heap with the first element
      temp = Array[i];
      Array[i] = Array[0];
      Array[0] = temp;

      //exclude the last element from the heap and rebuild the heap 
      heapify(Array, i-1, 0);
    }
  }

  // heapify function is used to build the max heap
  // max heap has maximum element at the root which means
  // first element of the array will be maximum in max heap
  static void heapify(int Array[], int n, int i) {
    int max = i;
    int left = 2*i + 1;
    int right = 2*i + 2;

    //if the left element is greater than root
    if(left <= n && Array[left] > Array[max]) {
      max = left;
    }

    //if the right element is greater than root
    if(right <= n && Array[right] > Array[max]) {
      max = right;
    }

    //if the max is not i
    if(max != i) {
      int temp = Array[i];
      Array[i] = Array[max];
      Array[max] = temp;
      //Recursively heapify the affected sub-tree
      heapify(Array, n, max); 
    }
  }

  // function to print array
  static void PrintArray(int Array[]) { 
    int n = Array.length; 
    for (int i=0; i<n; i++)   
      System.out.print(Array[i] + " "); 
    System.out.println(); 
  } 

  // test the code
  public static void main(String[] args) {
    int[] MyArray = {10, 1, 23, 50, 7, -4};
    int n = MyArray.length;
    System.out.println("Original Array");
    PrintArray(MyArray);

    heapsort(MyArray);
    System.out.println("\nSorted Array");
    PrintArray(MyArray); 
  }
}

The above code will give the following output:

Original Array
10 1 23 50 7 -4 

Sorted Array
-4 1 7 10 23 50

#include <iostream>
using namespace std;

static void heapsort(int Array[], int n);
static void heapify(int Array[], int n, int i);
static void PrintArray(int Array[], int n);

// function for heap sort which calls heapify function 
// to build the max heap and then swap last element of 
// the max-heap with the first element
// exclude the last element from the heap and rebuild the heap
static void heapsort(int Array[], int n) {
  int temp;
  for(int i = n/2; i >= 0; i--) {
    heapify(Array, n-1, i);
  }
  for(int i = n - 1; i >= 0; i--) {
    //swap last element of the max-heap with the first element
    temp = Array[i];
    Array[i] = Array[0];
    Array[0] = temp;

    //exclude the last element from the heap and rebuild the heap 
    heapify(Array, i-1, 0);
  }
}

// heapify function is used to build the max heap
// max heap has maximum element at the root which means
// first element of the array will be maximum in max heap
static void heapify(int Array[], int n, int i) {
  int max = i;
  int left = 2*i + 1;
  int right = 2*i + 2;

  //if the left element is greater than root
  if(left <= n && Array[left] > Array[max]) {
    max = left;
  }

  //if the right element is greater than root
  if(right <= n && Array[right] > Array[max]) {
    max = right;
  }

  //if the max is not i
  if(max != i) {
    int temp = Array[i];
    Array[i] = Array[max];
    Array[max] = temp;

    //Recursively heapify the affected sub-tree
    heapify(Array, n, max); 
  }
}

//function to print array
static void PrintArray(int Array[], int n) { 
  for (int i=0; i<n; i++)  
    cout<<Array[i]<<" "; 
  cout<<"\n"; 
} 

//test the code
int main (){
  int MyArray[] = {10, 1, 23, 50, 7, -4};
  int n = sizeof(MyArray) / sizeof(MyArray[0]); 
  cout<<"Original Array\n";
  PrintArray(MyArray, n);

  heapsort(MyArray, n);
  cout<<"\nSorted Array\n";
  PrintArray(MyArray, n);
  return 0;
}

The above code will give the following output:

Original Array
10 1 23 50 7 -4 

Sorted Array
-4 1 7 10 23 50

#include <stdio.h>

static void heapsort(int Array[], int n);
static void heapify(int Array[], int n, int i);
static void PrintArray(int Array[], int n);

// function for heap sort which calls heapify function 
// to build the max heap and then swap last element of 
// the max-heap with the first element
// exclude the last element from the heap and rebuild the heap
static void heapsort(int Array[], int n) {
  int temp;
  for(int i = n/2; i >= 0; i--) {
    heapify(Array, n-1, i);
  }
  for(int i = n - 1; i >= 0; i--) {
    //swap last element of the max-heap with the first element
    temp = Array[i];
    Array[i] = Array[0];
    Array[0] = temp;

    //exclude the last element from the heap and rebuild the heap 
    heapify(Array, i-1, 0);
  }
}

// heapify function is used to build the max heap
// max heap has maximum element at the root which means
// first element of the array will be maximum in max heap
static void heapify(int Array[], int n, int i) {
  int max = i;
  int left = 2*i + 1;
  int right = 2*i + 2;

  //if the left element is greater than root
  if(left <= n && Array[left] > Array[max]) {
    max = left;
  }

  //if the right element is greater than root
  if(right <= n && Array[right] > Array[max]) {
    max = right;
  }

  //if the max is not i
  if(max != i) {
    int temp = Array[i];
    Array[i] = Array[max];
    Array[max] = temp;
    //Recursively heapify the affected sub-tree
    heapify(Array, n, max); 
  }
}

// function to print array
static void PrintArray(int Array[], int n) { 
  for (int i=0; i<n; i++)  
    printf("%i ",Array[i]); 
  printf("\n"); 
} 

// test the code
int main () {
  int MyArray[] = {10, 1, 23, 50, 7, -4};
  int n = sizeof(MyArray) / sizeof(MyArray[0]); 
  printf("Original Array\n");
  PrintArray(MyArray, n);

  heapsort(MyArray, n);
  printf("\nSorted Array\n");
  PrintArray(MyArray, n);
  return 0;
}

The above code will give the following output:

Original Array
10 1 23 50 7 -4 

Sorted Array
-4 1 7 10 23 50

using System;
 
class MyProgram {
  // function for heap sort which calls heapify function 
  // to build the max heap and then swap last element of 
  // the max-heap with the first element
  // exclude the last element from the heap and rebuild the heap
  static void heapsort(int[] Array) {
    int n = Array.Length;
    int temp;
    for(int i = n/2; i >= 0; i--) {
      heapify(Array, n-1, i);
    }
    for(int i = n - 1; i >= 0; i--) {
      //swap last element of the max-heap with the first element
      temp = Array[i];
      Array[i] = Array[0];
      Array[0] = temp;

      //exclude the last element from the heap and rebuild the heap 
      heapify(Array, i-1, 0);
    }
  }

  // heapify function is used to build the max heap
  // max heap has maximum element at the root which means
  // first element of the array will be maximum in max heap
  static void heapify(int[] Array, int n, int i) {
    int max = i;
    int left = 2*i + 1;
    int right = 2*i + 2;

    //if the left element is greater than root
    if(left <= n && Array[left] > Array[max]) {
      max = left;
    }

    //if the right element is greater than root
    if(right <= n && Array[right] > Array[max]) {
      max = right;
    }

    //if the max is not i
    if(max != i) {
      int temp = Array[i];
      Array[i] = Array[max];
      Array[max] = temp;
      //Recursively heapify the affected sub-tree
      heapify(Array, n, max); 
    }
  }
       
  // function to print array
  static void PrintArray(int[] Array) { 
    int n = Array.Length; 
    for (int i=0; i<n; i++)   
      Console.Write(Array[i] + " "); 
    Console.Write("\n"); 
  } 

  // test the code
  static void Main(string[] args) {
    int[] MyArray = {10, 1, 23, 50, 7, -4};
    Console.Write("Original Array\n");
    PrintArray(MyArray);

    heapsort(MyArray);
    Console.Write("\nSorted Array\n");
    PrintArray(MyArray);  
  }
}

The above code will give the following output:

Original Array
10 1 23 50 7 -4 

Sorted Array
-4 1 7 10 23 50

<?php
// function for heap sort which calls heapify function 
// to build the max heap and then swap last element of 
// the max-heap with the first element
// exclude the last element from the heap and rebuild the heap
function heapsort(&$Array, $n) {
  for($i = (int)($n/2); $i >= 0; $i--) {
    heapify($Array, $n-1, $i);
  }
  for($i = $n - 1; $i >= 0; $i--) {
    //swap last element of the max-heap with the first element
    $temp = $Array[$i];
    $Array[$i] = $Array[0];
    $Array[0] = $temp;

    //exclude the last element from the heap and rebuild the heap 
    heapify($Array, $i-1, 0);
  }
}

// heapify function is used to build the max heap
// max heap has maximum element at the root which means
// first element of the array will be maximum in max heap
function heapify(&$Array, $n, $i) {
  $max = $i;
  $left = 2*$i + 1;
  $right = 2*$i + 2;

  //if the left element is greater than root
  if($left <= $n && $Array[$left] > $Array[$max]) {
    $max = $left;
  }

  //if the right element is greater than root
  if($right <= $n && $Array[$right] > $Array[$max]) {
    $max = $right;
  }

  //if the max is not i
  if($max != $i) {
    $temp = $Array[$i];
    $Array[$i] = $Array[$max];
    $Array[$max] = $temp;
    //Recursively heapify the affected sub-tree
    heapify($Array, $n, $max); 
  }
}

// function to print array
function PrintArray($Array, $n) { 
  for ($i = 0; $i < $n; $i++) 
    echo $Array[$i]." "; 
  echo "\n"; 
} 

// test the code
$MyArray = array(10, 1, 23, 50, 7, -4);
$n = sizeof($MyArray); 
echo "Original Array\n";
PrintArray($MyArray, $n);

heapsort($MyArray, $n);
echo "\nSorted Array\n";
PrintArray($MyArray, $n);
?>

The above code will give the following output:

Original Array
10 1 23 50 7 -4 

Sorted Array
-4 1 7 10 23 50

Time Complexity:

The time complexity of creating a heap is Θ(N) and time complexity of creating a max heap is Θ(logN) and overall time complexity of heap sort is Θ(NlogN).

AlphaCodingSkills

AlphaCodingSkills Android App

AlphaCodingSkills is a online learning portal that provides tutorials on Python, Java, C++, C, C#, PHP, R, Ruby, Rust, Scala, Swift, Perl, SQL, Data Structures and Algorithms. Tutorials, examples, references and content of the website are reviewed and simplified continuously to improve comprehensibility and eliminate any possible error. We use cookies to ensure best browsing experience on our website. While using this website, you acknowledge to have read and accepted our cookie and privacy policy.